

10.12.2012 /Статьи
В статье рассматривается метод расчета системы массового обслуживания при произвольных законах распределения входных процессов и процессов обслуживания.
The article addresses the method for calculating a queuing network at random law distribution of input processes and service processes.
Ключевые слова: мультисервисная сеть доступа, самоподобный трафик, система массового обслуживания типа G/G/m, диффузионная аппроксимация.
Key words: self-similar traffic, queuing network of G/G/m type, diffusive approximation.
Высокая активность пользователей современных телекоммуникационных сетей специального назначения, предоставляющих различным категориям пользователей широкий спектр услуг связи (т.н. мультисервисные сети доступа (МСД) [1,2]), обуславливает необходимость передавать максимальное количество сообщений с заданным качеством. В мультисервисных сетях доступа поддержание необходимых режимов функционирования отдельных элементов и системы в целом должно осуществляться под управлением АСУ сетью, которое предполагает решение задач эффективного управления информационным обменом. Одна из наиболее сложных и важных подзадач является задача управления информационными потоками, реализуемая (в соответствии с концепцией TMN) на уровне управления сетью [3].
Потоки, циркулирующие в мультисервисной сети, характеризуются неоднородностью и существенной нестационарностью. Они представляют собой сумму определенного множества потоков, поступающих в сети доступа из различных вторичных сетей связи: потоки требований на установление соединений (в т.ч. виртуальных) для речевого обмена (телефонные сети, сети на технологии ISDN и т.д.), потоки сообщений и пакетов (сети передачи данных, документального обмена, обмена данными) как в режиме дейтаграммной передачи, так и в режиме установления виртуальных соединений, потоки мультимедиа информации, характеризующиеся пачечным характером трафика. [4]. Подобное поведение трафика в сети исследуется с помощью самоподобных процессов.
В работах [5-7] приведены подробные доказательства структуры самоподобного трафика, появляющегося вследствие объединения новых и существующих технологий передачи и коммутации с разнородными потоками сервисов и приложений, а также причины появления самоподобных свойств. Следствием этих факторов является выраженная пачечность интенсивности трафика. Появление мощных пиковых скачков интенсивности в часы наибольшей нагрузки вызывает значительные потери пакетов и появление длительных задержек в сети, что сказывается на качестве обслуживания пользователей.
Таким образом, данные показатели качества обслуживания трафика (вероятность потери пакета, время задержки) необходимо исследовать для повышения производительности мультисервисной сети доступа.
Приведенные факторы определяют актуальность дальнейшего расчета показателей качества обслуживания МСД.
Анализ отечественных и зарубежных работ [5-10] показывает, что для описания трафика в мультисервисных IP-сетях специального назначения целесообразно использовать распределение Парето. Для трафика приложений ограниченно используются распределения Вейбулла, логнормальное и пуассоновское.
При этом, распределение Парето, как и распределения Вейбулла и логнормальное, относится к распределениям с так называемым “тяжелым хвостом” и обладает бесконечной дисперсией в диапазоне 1<a<2, где показатель a характеризует «тяжесть» хвостов распределения и определяет пачечную структуру процесса. Такие процессы считаются самоподобными.
При этом допущении поведение трафика мультисервисной IP-сети можно охарактеризовать различными законами распределения, отличными от пуассоновского, в основном, законом Парето[11].
Вследствие изложенного, целесообразно в качестве модели системы массового обслуживания (СМО) выбрать систему с общими распределениями входного потока и процессов обслуживания типа G/G/m (система с произвольным распределением). Задача расчета систем вида G/G/m для указанных входных процессов и процессов обслуживания (Парето, Вейбулла, логнормального) затруднена тем, что дисперсии этих процессов бесконечны. Учитывая широкое применение закона Парето для описания трафика в IP-ориентированных сетях, рассматривается только система с данным распределением.
Для формализации трафика мультисервисной сети связи можно разделить его на три класса: трафик реального времени, потоковый и эластичный.
Для пакетного трафика рассматривается общая задержка t3 (или время доставки пакета) как сумма транспортной задержки tmp, задержки распространения tp, задержки коммутации tкомм и задержки при организации очередей в маршрутизаторах tоч (времени задержки в узле):

В случае, если сеть не испытывает перегрузки, задержка при организации очередей в маршрутизаторах tоч отсутствует. В этом случае можно говорить о минимально возможной задержке при передаче пакетов через заданную сеть. В случае перегрузки сети tоч не только может составить значительную величину, но и приводит к джиттеру задержки. Джиттер задержки и определяет максимальную задержку на приеме. В зависимости от типа приложения, принимающая сторона может попытаться компенсировать джиттер задержки за счет организации приемного буфера для хранения принятых пакетов на время tдж, меньше и равное верхней границе дрожания.
Для трафика реального времени джиттер задержки может привести к потере пакетов, т.к. при превышении порогового значения задержки пакеты будут отброшены как не удовлетворяющие требованиям, предъявляемым к режиму реального времени. Для потокового трафика внесение дополнительной задержки не оказывается критичным и не приводит к потерям.
Для представления математической модели расчета показателей качества вводится ограниченное распределение случайной величины, которое позволяет, не меняя формы распределения, указать ее минимальное и максимальное значения [13]. Если случайная величина x – размер блока данных, то диапазон изменений такой величины (0; L), где L – максимально возможный размер блока (пакет или несколько пакетов), отличный от бесконечности. Тогда плотность распределения вероятности:

где 0<α<2 - параметр распределения Парето.
C помощью пределов интегрирования формула (2) принимает вид:

где k – минимальный размер блока данных,
L- максимально возможный размер блока, отличный от бесконечности.
Плотность распределения вероятности для ограниченного распределения Парето
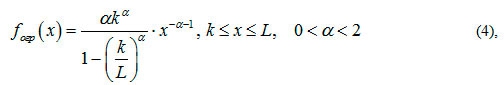
Тогда основные параметры распределения Парето будут иметь следующий вид (формулы 5-6):
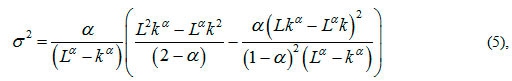
где σ2 - дисперсия функции распределения Парето;
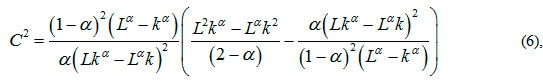
С2 - квадратичный коэффициент вариации функции распределения Парето.
Для расчета вероятности потери пакета и времени задержки в системе G/G/m используются результаты теории диффузионной аппроксимации, полученные в [14].
Диффузионная аппроксимация является наиболее известным и широко применяемым методом приближенного расчета СМО при произвольных законах распределения входных процессов и процессов обслуживания. Идея метода заключается в аппроксимации дискретного случайного процесса (в данном случае – описывающего количество пакетов в узлах) непрерывным диффузионным процессом. Стоит отметить, что в области низких нагрузок данный метод дает заметную погрешность. Погрешность диффузионной аппроксимации также возрастает с увеличением коэффициента вариации распределений.
Таким образом, для расчета показателей качества обслуживания системы с произвольным распределением (в данном случае – распределение Парето P/P/m) метод диффузионной аппроксимации может использоваться, если коэффициент вариации функции распределения случайной величины больше 1. Согласно [14], дальнейшая задача расчета показателей качества обслуживания состоит в целесообразности определения квадратичного коэффициента вариации.
Литература
1. Закон РФ «О связи», 2003 г.
2. Концептуальные положения по мультисервисным сетям связи РФ. 2001 г.
3. Олифер В. Г., Олифер Н. А. Компьютерные сети: Принципы, технологии, протоколы. СПб.: Питер, 2000. 668с.
4. Буренин А.Н. Формализация задачи оптимального управления потоками в мультисервисной сети связи // Проблемы внедрения новых сетевых технологий в системы связи ВС РФ. Сборник научных трудов. СПб.: АРПИУ, 2005. Вып. 7. С. 59-64.
5. Шелухин О. И., Тенякшев А. М., Осин А. В. Фрактальные процессы в телекоммуникациях.- М.:Радиотехника,2003. 479 с.
6. Шелухин О. И., Тенякшев А. М., Осин А. В. Моделирование информационных систем:- М. Радиотехника, 2005. 368 с.
7. Шелухин О. И., Осин А. В., Смольский С. М. Самоподобие и фракталы. Телекоммуникационные приложения.- М.: Физматлит, 2008., 368 с.
8. Downey A. B. Lognormal and Pareto distributions in the Internet. www.allendowney.com/research/longtail/downey03lognormal.pdf, 2003.
9. Minoli D., Minoli E. Delivering Voice over IP Networks. Jonh Willey&Sons, Inc., 1998.
10. Molnar S., Dang T.D. Scaling Analysis of IP Components. ITC Specialist,
Birkhauser, Boston , 2003.
11. Сорокина Е.А., Яровикова О.В. Методы моделирования мультисервисных сетей связи // Техника радиосвязи. Научно- технический сборник. Омск.: ОНИИП, 2009. Вып. 14. С.101-105.
12. Сорокина Е.А., Гель В.Э., Щедров А.С. Обоснование метода для расчета показателей качества обслуживания мультисервисной сети доступа специального назначения // Новые информационные технологии в системах связи и управления. Труды IX Российской научно-технической конференции. Калуга: Изд-во научной литературы Н. Ф. Бочкаревой, 2010. С. 80-84.
13. Симонина О.А., Галкин А.М. Метод расчета характеристик IP-ориентированных мультисервисных сетей с учетом свойств самоподобия трафика // Труды учебных заведений связи / СПбГУТ. СПб. 2005. № 172. С. 6-10.
14. Зелигер Н.Б., Чугреев О.С., Яновский Г.Г. Проектирование сетей и систем передачи дискретных сообщений. М.: Радио и связь, 1984.173 с.