МЕТОДЫ МОДЕЛИРОВАНИЯ МУЛЬТИСЕРВИСНЫХ СЕТЕЙ СВЯЗИ

12.11.2012 /Статьи

В статье представлены методы математического моделирования, позволяющие исследовать работу мультисервисной сети связи. 

The article presents the mathematical modelling methods that allow studying operations of a multi-service communications network.

Ключевые слова: моделирование для обслуживания сети, аналитические модели, имитационные модели, системы массового обслуживания (СМО), сети массового обслуживания, типы СМО, метод диффузионного приближения, анализатор протоколов.

Key words: analytical models, simulation models ,queuing networks.

Чаще всего под моделированием подразумевают построение математической модели, которая имеет вид функциональной зависимости

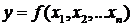
В качестве функции f можно рассматривать такой  показатель эффективности системы, как, например,  полезную  скорость передачи данных, а в качестве параметров x_i- все параметры данной сети, от которых зависит f.

Целесообразно для полного описания функционирования мультисервисной сети (МСС) рассматривать набор характеристик, позволяющий действительно оценить состояние системы по необходимым критериям. Таким образом, для полного исследования МСС часто приходится строить большой набор математических моделей, которые должны друг другу не противоречить, но, конечно, могут быть разными по структуре.

Существует ряд методов математического моделирования работы МСС, но конечный полученный теоретический результат, очевидно, не должен отличаться от экспериментального.

Итак, для глубокого понимания работы любой МСС необходимо провести два основных этапа исследования: теоретический и  экспериментальный, и результаты  сравнить. Для теоретического исследования применяют один из видов математического моделирования (аналитический или имитационный), для экспериментального – измерения при помощи анализаторов протоколов [1, 2, 3]. Модели исследуемой сети отличаются между собой, прежде всего уровнем использования математического аппарата.

Аналитические модели описания работы МСС, как правило, строятся на основе понятий аппарата теорий массового обслуживания, теории вероятностей и Марковских процессов, а также методов диффузной аппроксимации и декомпозиции [4]. Могут также применяться дифференциальные и алгебраические уравнения. Они требуют оперирования со строгими математическими терминами. В результате такого подхода можно получить решения для определенных задач мониторинга состояния сети, но математические упрощения, положенные в основу построения модели, часто не дают реальной картины происходящего, да и вычисления могут быть довольно громоздкими. Такими методиками целесообразно пользоваться при оценке работы МСС в первом приближении [4].

Имитационные модели описывают объект исследования на некотором языке, который отображает элементарные явления, составляющие функционирование исследуемой системы с сохранением их логической структуры, последовательности протекания во времени, особенностей и состава информации о состоянии процесса. Алгоритмы, заложенные в основе имитационных моделей, почти точно воссоздают работу реальных устройств в сети, что позволяет на их основе строить комплексы моделирования МСС, например,  с помощью пакета NetworkSimulator2 (ns2).

Получение аналитических моделей возможно в случае простых  вычислительных систем. В связи  с этим большинство реально встречающихся задач по анализу систем решается имитационными методами, а аналитические модели используются для ориентировочных оценок и в процедурах оптимизации, требующих высокого быстродействия и небольшой точности. Следует отметить, что в одну и ту же модель могут одновременно входить подмодели обоих типов. При аналитическом моделировании исследование процессов или объектов заменяется построением их математических моделей и исследованием этих моделей. В основу метода положены идентичность формы уравнений и однозначность соотношений между переменными в уравнениях, описывающих оригинал и модель. Поскольку события, происходящие в МСС, носят случайный характер, то для их изучения наиболее подходящими являются вероятностные математические модели теории массового обслуживания. Объектами исследования в теории массового обслуживания являются системы массового обслуживания (СМО) и сети массового обслуживания (СеМО).

Системы массового обслуживания классифицируются по следующим признакам:

1) закону распределения входного потока заявок;

2) числу обслуживающих приборов;

3) закону распределения времени обслуживания в обслуживающих приборах;

4) числу мест в очереди;

5) дисциплине обслуживания.

Для краткости записи при обозначении любой СМО принята система кодирования A/B/C/D/E, где на месте буквы ставятся соответствующие характеристики СМО:

A – закон распределения интервалов времени между поступлениями заявок. Наиболее часто используются следующие законы распределения: экспоненциальное (H), гамма-распределение (Г), детерминированное (D).

Для обозначения произвольного характера распределения используется символ G;

B – закон распределения времени обслуживания в приборах СМО. Здесь также приняты такие же обозначения, как и для распределения интервалов между поступлениями заявок;

C – число обслуживающих приборов. Здесь приняты следующие обозначения: для одноканальных систем записывается 1, для многоканальных в общем случае – k (число каналов);

D – число мест в очереди. Если число мест в очереди не ограничено, то данное обозначение может опускаться. Для конечного числа мест в очереди в общем случае приняты обозначения r  или n (число мест);

E – дисциплина обслуживания. Наиболее часто используются следующие варианты дисциплины обслуживания: FIFO (первым пришел - первым вышел), RANDOM (случайный порядок обслуживания). При дисциплине обслуживания FIFO данное обозначение может опускаться.

Для моделирования МСС наиболее часто используются следующие типы СМО:

1. одноканальные СМО с ожиданием – представляют собой один обслуживающий прибор с бесконечной очередью. Данная СМО является наиболее распространенной при моделировании. С той или иной долей приближения с ее помощью можно моделировать практически любой узел МСС;
2. Одноканальные СМО с потерями – представляют собой один обслуживающий прибор с конечным числом мест в очереди. Если число заявок превышает число мест в очереди, то лишние заявки теряются. Этот тип СМО может быть использован при моделировании каналов передачи в МСС;
3. многоканальные СМО с ожиданием – представляют собой несколько параллельно работающих обслуживающих приборов с общей бесконечной очередью. Данный тип СМО часто используется при моделировании групп абонентских терминалов МСС, работающих диалоговом режиме;
4. многоканальные СМО с потерями – представляют собой несколько параллельно работающих обслуживающих приборов с общей очередью, число мест в которой ограничено. Эти СМО, как и одноканальные с потерями, часто используются для моделирования каналов связи в МСС;
5. одноканальные СМО с групповым поступлением заявок – представляют собой один обслуживающий прибор с бесконечной очередью. Перед обслуживанием заявки группируются в пакеты по определенному правилу;
6. одноканальные СМО с групповым обслуживанием заявок – представляют собой один обслуживающий прибор с бесконечной очередью. Заявки обслуживаются пакетами, составляемыми по определенному правилу.

МСС может быть представлена в виде сети массового обслуживания. Различают экспоненциальные и неэкспоненциальные модели МСС. Экспоненциальные модели основаны на предположении о том, что потоки заявок, поступающие в МСС, являются пуассоновскими, а время обслуживания в узлах доступа МСС имеет экспоненциальное распределение. Для таких сетей получены точные методы для определения их характеристик; трудоемкость получения решения зависит в основном от размерности сети.

Однако в большинстве сетей (и локальных сетей в частности) потоки не являются пуассоновскими. Модели таких сетей называются неэкспоненциальными. При анализе неэкспоненциальных сетей в общем случае отсутствуют точные решения, поэтому наибольшее применение здесь находят приближенные методы.

Одним из таких методов является метод диффузионной аппроксимации. Использование диффузионной аппроксимации позволило к настоящему времени получить приближенные аналитические зависимости для определения характеристик СМО. При этом не требуется точного знания функций распределения случайных величин, связанных с данной СМО (интервалов между поступлениями заявок, временем обслуживания в приборах), а достаточно только знание первого (математического ожидания) и второго (дисперсии или квадрата коэффициента вариации) моментов этих величин.

Применение диффузионной аппроксимации при анализе МСС основано на следующем:

1. по каждому типу заявок вычисляется интенсивность поступления заявок данного типа в узлы сети так, как если бы данный поток заявок циркулировал в сети только один;
2. по определенному правилу, зависящему от типа СМО и дисциплины обслуживания, складываются потоки заявок от всех источников;
3. по определенному правилу определяется среднее время обслуживания в каждом узле МСС;
4. полученные значения подставляются в соответствующую диффузионную формулу и определяются характеристики узлов МСС;
5. определяются характеристики МСС в целом.

Обычно при моделировании работы МСС используют  набор  характеристик, а результат моделирования выражен в получении средних значений и дисперсий тех величин, о которых необходима информация, описывающая  систему наиболее полно.

Для получения же точных результатов, отражающих реальное состояние МСС, необходимо проводить статическую обработку эксперимента. Экспериментом в данном случае является либо запись показаний параметров при реальной работе сети, либо запись показаний параметров в режиме модуляции реальной работы. И в том, и в другом случае в качестве средства записи используют схожие инструменты, но почти все они построены по принципу анализатора протоколов [3].

Анализатор протоколов представляет собой аппаратный, либо программно-аппаратный комплекс, который позволяет пользователям захватывать и обрабатывать данные, передаваемые в конкретной МСС. По расшифровке полученной таким образом информации, наблюдатель может делать вывод о реальном состоянии МСС. Для полного понимания работы анализатора протоколов, конечно, необходимо обладать знаниями о физическом распространении сигналов в канале связи, о форме их представления, о методах кодировки, о структуре передачи данных. Во многих приложениях такого класса такие сведения бывают неполными, поэтому часто приходится придумывать методики, позволяющие выражать требуемые параметры анализатором протоколов.

Если структурная топология МСС позволяет получать данные от каждого активного узла в любой точке системы, то накопленная анализатором протоколов в любом месте статистика отражает реальное состояние сети. В сетях с более сложной топологией используют зонды, которые представляют собой модули, пересылающие необходимую информацию от неохваченных записью участков сети в места установки сетевого анализатора протоколов.

 

Литература

 

1. Бушуев С.Н., Осадчий А.С., Фролов В.М. Теоретические основы создания информационно-технических систем. СПб: ВАС, 1998, с.404.
2. Ю.С. Исаченко. Анализаторы протоколов для NGN// Вестник связи, №9, 2006 г.
3. Н.А. Олифер, В.Г. Олифер. Роль коммуникационных протоколов и функциональное назначение основных типов оборудования корпоративных сетей. Центр информационных технологий – www.citforum.ru/ nets/ protocols/index.shtml
4.  http:// www.badmivasil.ru/ index1.htm. Бадмильсон В.Н. Лекции по математическому моделированию.